Diffie-Helman Key Exchange

Diffie-Hellman key exchange is a mechanism that allows two parties to create a shared secret key based on some privately kept information (numbers) and some publicly exchanged information (numbers). It is a key agreement protocol in which all participants contribute equally to generate the secret key.

The below diagram illustrates how Diffie-Hellman works in a non-mathematical way.

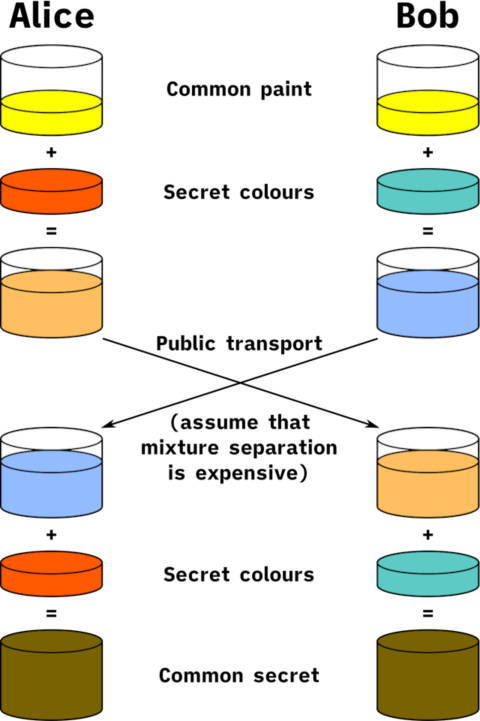
The critical part is that it is impossible to reverse back to the two secret colours that formed the mixture by only knowing one colour and the mixture. The two secret colours were never revealed to the public.

The maths behind Diffie-Hellman is very elegant. Two parties agree on a generator $g$ and a 2048-4096-bit long number $n$. $g$ is sometimes pre-defined in the algorithm to simplify the process further. One party chooses a random number $a$ between $1-n$ and performs the operation $g^a$ mod $n$; the other party performs the same operation with a random number $b$; the two parties then exchange the results publicly and perform the operation $g^{(a)b}$ mod $n$ and $g^{(b)a}$ mod $a$, respectively. This results in a shared number between $1-n$ (the symmetric key) that is only known to the two parties as long as $a$ and $b$ are kept secret. The public cannot guess it easily when n is large enough.

Reference

• Computerphile (2017). Secret Key Exchange (Diffie-Hellman) - Computerphile . YouTube. Available at: https://www.youtube.com/watch?v=NmM9HA2MQGI.